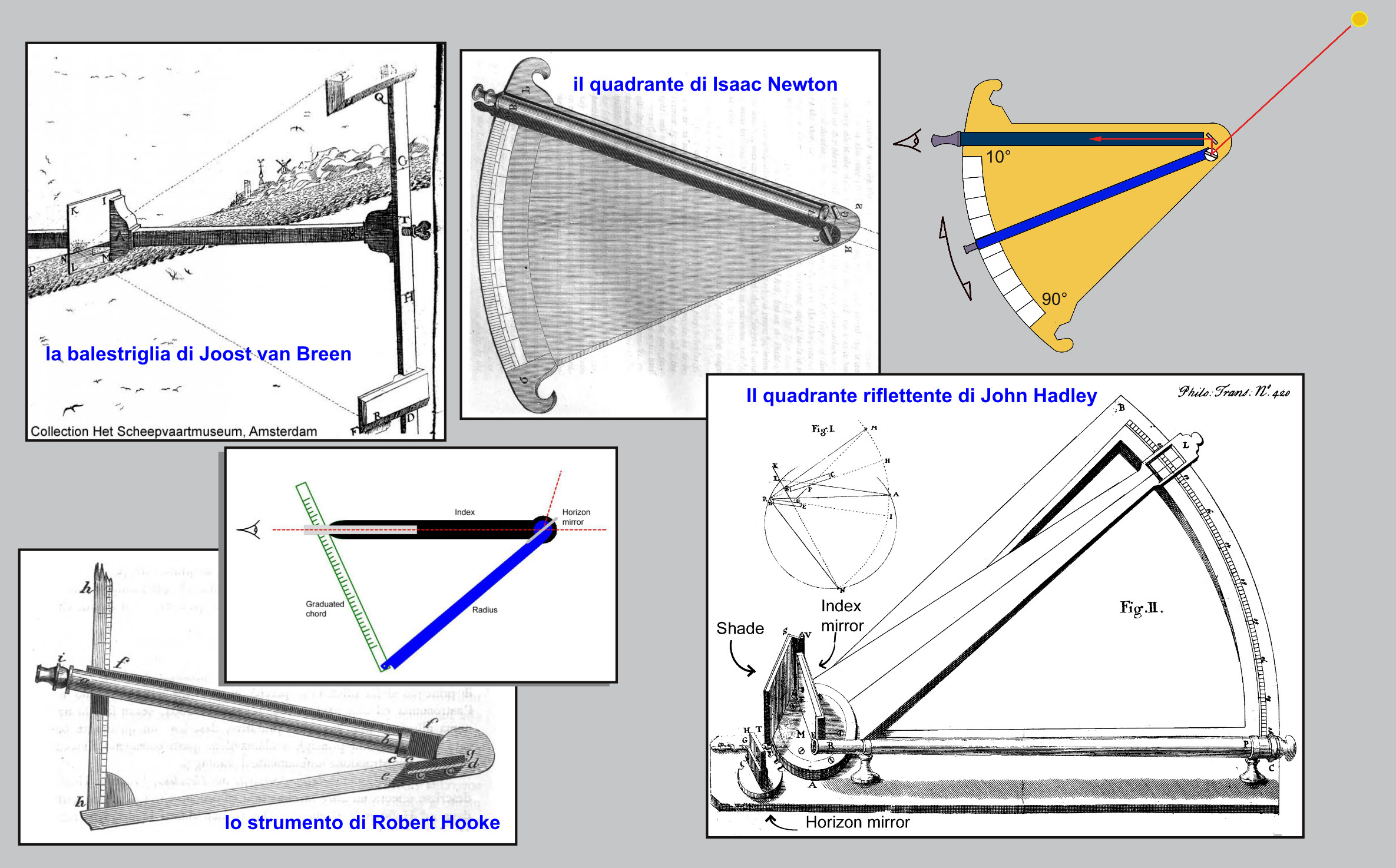
Dalla presentazione presso la Royal Society dell’ottante di Hadley nel 1731, si dovrà attendere il 1750 perché lo strumento si diffondesse prima nella marina inglese e successivamente nelle altre marine. Inizialmente l’ottante, non sempre dotato di cannocchiale, era di grandi dimensioni (raggio di circa 50 cm) per limitare gli errori della scala, struttura in legno duro, specchi in metallo, alidada in rame e lembo in avorio.
Nello stesso anno (1730) in cui Hadley inventava il suo ottante, anche l’americano Thomas Godfrey (1704-1749) inventò uno strumento simile e ritenendo la sua invenzione originale ne trasmise una dettagliata descrizione alla Royal Society. In verità si scoprì poi, nel 1742, che la paternità dell’invenzione era stata di Newton.
L’ottante in pochi anni subì numerose modifiche, dalla disposizione verticale per un più facile uso, fino alla forma tipica del sestante in cui l’ampiezza dell’arco graduato fu portata da 45° a 60°, come aveva suggerito nel 1757 il vice ammiraglio inglese John Campbell (1720-1790), marinaio e uomo di scienza. Successivamente l’arco del lembo fu portato a 80°
Con
la realizzazione delle prime macchine a dividere e gli ulteriori
progressi tecnologici
iniziati
a partire dagli ultimi anni del ‘700 (per un approfondimento ved.
l’articolo sull’evoluzione degli strumenti nautici) il
sestante raggiunse nel corso di
quello scorcio di fine secolo e degli inizi dell’800
già un
alto grado di perfezione.
I
principali protagonisti del
progresso di un così importante
strumento per la navigazione astronomica furono gli inglesi e i
tedeschi, tra cui l’ottico
inglese Jesse
Ramdsen (1735-1800),
il
tedesco Georg
von Reichenbach (1772-1826),
l’inglese
Edward
Troughton (1753-1835)
Nota: quando il traguardo è l’orizzonte l’altezza α = 0 e i raggi incidenti e riflessi dagli specchi formano un angolo β rispetto alla normale agli specchi stessi. Poichè lo specchio piccolo è fisso i due raggi incidente e riflesso non cambiano di posizione (altrimenti il target non sarebbe osservabile). Quando il traguardo ha un angolo α > 0 lo specchio grande deve ruotare e quindi ruota la sua normale. L’angolo γ formato tra le due normali allo specchio grande (corrispondenti alle due posizioni) ha lo stesso valore dell’angolo percorso dall’alidada. Con semplici passaggi si ricava che l’angolo percorso dall’alidada è la metà dell’altezza α, quindi una escursione di 60° dell’alidada corrisponde a 120° di apertura.