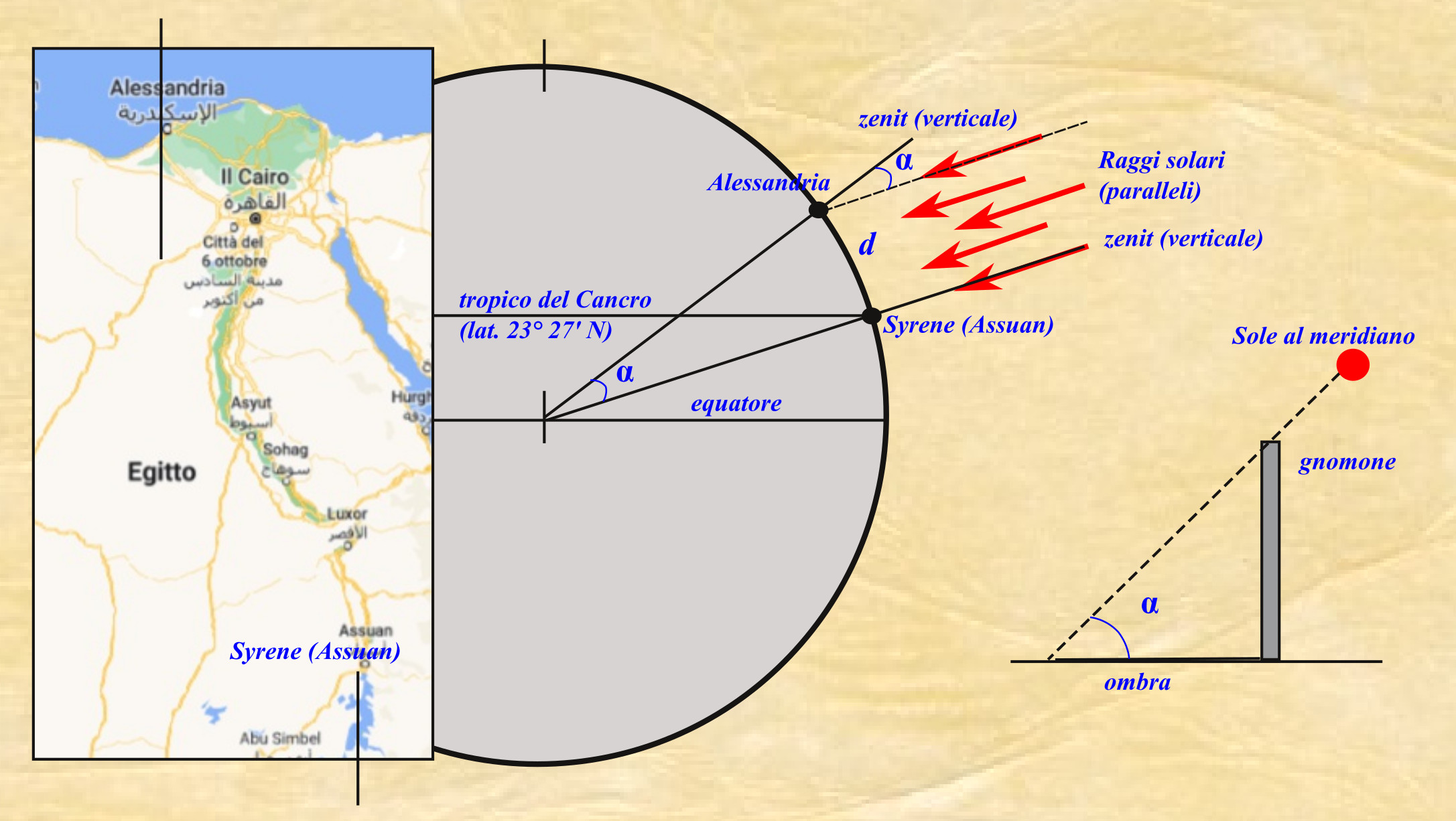
Nel IV sec. a.C., una volta accettata l’idea di una Terra sferica, un’ipotesi risalente a quasi due secoli prima di Parmenide e Pitagora, si pose il problema di conoscerne le dimensioni. Diversi astronomi si cimentarono nel valutare quanto fosse grande, ma sicuramente la più nota determinazione fu quella di Eratostene di Cirene (III sec. a.C.), direttore della biblioteca di Alessandria in Egitto, che applicò un ingegnoso metodo matematico geometrico la cui descrizione (quella originaria è andata perduta) è riportata in forma semplificata in due pagine del Caelestia, il trattato di astronomia di Cleomede, un astronomo greco vissuto circa due secoli dopo.
Eratostene sapeva che nel giorno del solstizio d’estate, mentre il Sole di mezzodì era allo zenit di Siene, tanto da illuminare come descrive Cleomede il fondo dei pozzi, ad Alessandria, stessa ora e giorno, i raggi solari formavano con la verticale un angolo che Eratostene aveva calcolato essere 1/50 della circonferenza, corrispondente all’arco di meridiano tra le due località. Nota in 5000 stadi la distanza tra i due luoghi, la lunghezza del meridiano risultava, con semplice proporzione, 50×5000 = 250.000 stadi.
Il racconto di Cleomede è solo indicativo del metodo adottato da Eratostene, che va letto tenendo conto del livello di conoscenze scientifiche di allora.
La storia dell’assenza di ombra a Siene rispetto ad Alessandria andrebbe interpretata come una notizia giunta ad Eratostene che dava conferma della sfericità della Terra piuttosto che l’occasione per l’esecuzione della misura. L’ipotesi più affascinante, segno di una visione geometrica e matematica del problema, fu quella di aver considerato i raggi solari paralleli, conseguenza di un Sole ritenuto assai lontano dalla superficie terrestre. La misura dell’inclinazione dei raggi solari, ottenuta con lo gnomone, fu ricavata in maniera diretta, con una corda tesa dall’estremità superiore dell’asta all’estremità dell’ombra e quindi impiegando un cerchio suddiviso in tante parti uguali, in effetti un goniometro. Si deve escludere un metodo indiretto (altezza e lungh. ombra) non tanto perché la trigonometria applicata ai triangoli comparirà molti secoli dopo, ma perché i metodi della corda (equivalente alla funzione seno) per essere applicati avevano bisogno di tabelle che compariranno con Ipparco di Nicea un secolo successivo. Poichè Siene non è sul tropico, ma appena più a nord, il valore di 1/50 è, con molta probabilità, la differenza degli angoli delle ombre letti agli gnomoni nelle due località nello stesso giorno di riferimento (ad esempio al solstizio).
Infatti il valore angolare espresso in frazioni misurato da Eratostene era 1/50 di 360° corrispondente a 7°,2 un valore del tutto corretto se si pensa che tra Alessandria e Assuan, l’odierna Siene, la differenza di latitudine è di 7°,1.
Si noti che i numeri decimali, la cui origine si deve ai matematici indiani, compariranno in Europa più di 1000 anni dopo attraverso l’evoluzione e tramissione da parte degli arabi e per il tramite dell’italiano Leonardo Pisano, detto Fibonacci (1170-1240).
La distanza tra le due località di 5000 stadi, invece, è affetta da errore (per eccesso) avendole considerate sullo stesso meridiano. A questo punto per poter comprendere lo scostamento del valore ricavato da Eratostene rispetto al valore stimato oggi del meridiano terrestre occorre conoscere quanto vale in metri uno stadio. E qui nascono i problemi. Secondo gli studiosi che si cimentarono alla fine dell’800 il valore sarebbe compreso tra 157,5 e 163 metri, valori che conducono ad un errore della misura di poco meno del ± 2%. Un risultato di tutto rispetto.
Coordinate delle due località:
Assuan 24,1° N 32,9° E
Alessandria 31,2° N 29,9° E