l primo esempio di giroscopio si deve al tedesco J.G. Federico Bohnenberger (1765-1831), professore di matematica, astronomia e fisica all’Università di Tubinga il quale lo realizzò nel 1815 per un uso didattico (in particolare per la spiegazione del fenomeno di precessione della Terra), chiamandolo semplicemente “Machine”. Acquisito dall’École Polytechnique di Parigi, su intervento del matematico Siméon-Denis Poisson (1781-1840), entrò in numerose scuole francesi per interesse dell’altro matematico francese Pierre-Simon Laplace (1749-1827).
Fu proprio la diffusione della “macchina di Bohnenberger” che sollecitò l’interesse di Léon Foucault (1819-1868) il quale nel 1852, dopo averne limitato il funzionamento a due gradi di libertà, ebbe modo di comprenderne l’uso anche come dimostratore della rotazione terrestre, così da coniare il nuovo termine giroscopio (dal greco giro-rotazione e scopos-a cui si guarda), termine poi rimasto anche quando il meccanismo è stato utilizzato per altre applicazioni.
Il giroscopio è fondamentalmente costituito da un corpo solido di rivoluzione di notevole inerzia (somma dei prodotti di ciascuna massa elementare per la corrispondente distanza dall’asse) capace di ruotare ad elevata velocità angolare intorno al proprio asse, convenzionalmente denominato X, noto anche come asse di spin.
Il rotore è montato su un sistema cardanico che permette anche le rotazioni intorno agli assi y e z.
Il giroscopio deve essere bilanciato, cioè il suo baricentro deve trovarsi all’intersezione dei tre assi della sospensione cardanica.
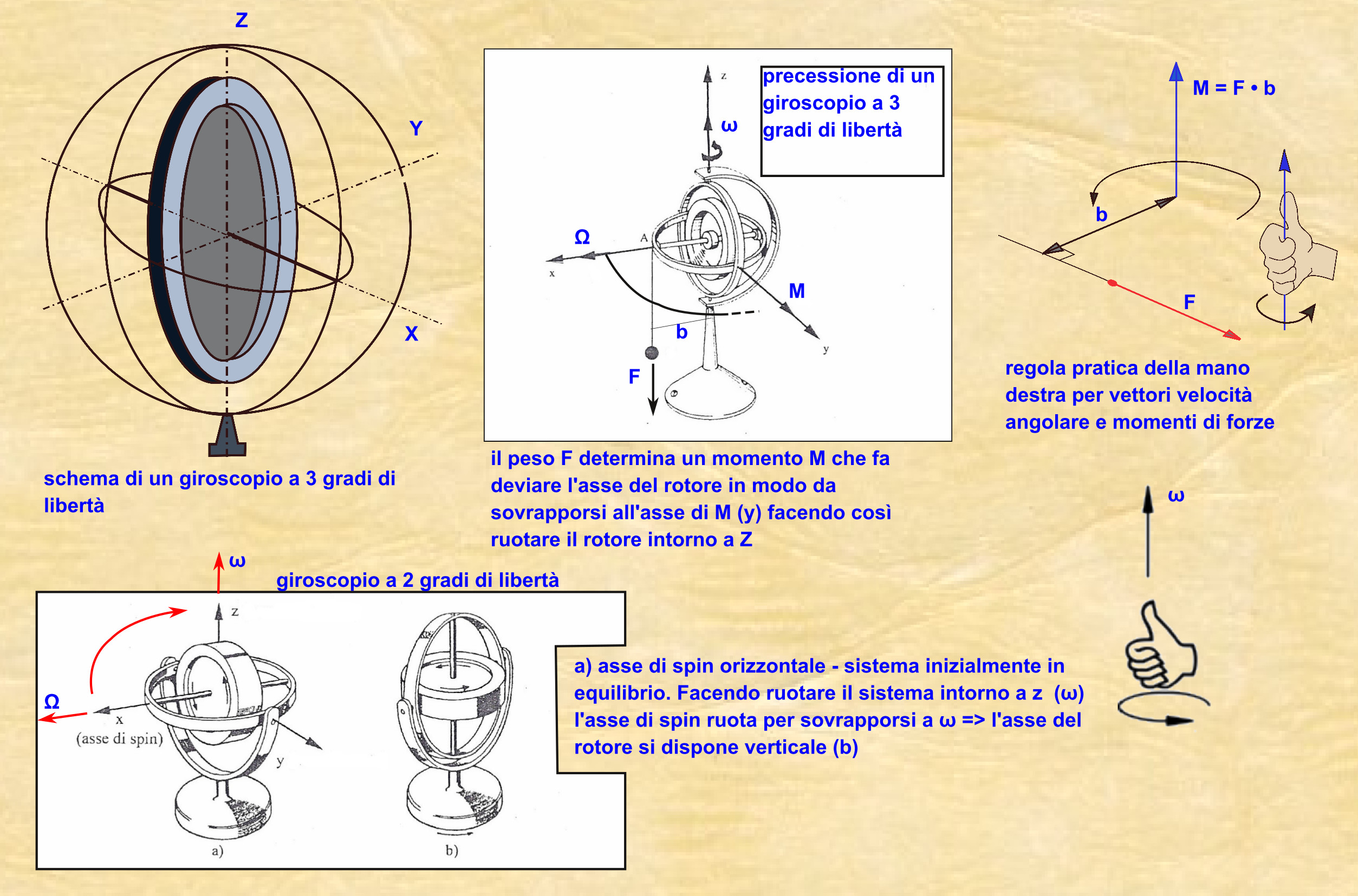
Il giroscopio così descritto, pemettendo le rotazioni secondo tre assi, è detto a 3 gradi di libertà. Se si blocca lo snodo cardanico intorno ad uno dei due assi Y o Z, al giroscopio rimangono 2 gradi di libertà.
Imprimendo velocità
angolare al rotore, questo presenterà un fenomeno noto come inerzia
o rigidità giroscopica che si manifesta nel mantenere
inalterata la posizione dell’asse di spin in una data direzione.
Se
inizialmente l’asse punta verso una stella, nel tempo tenderà ad
indicare sempre la medesima stella. Tale proprietà è tanto più
manifesta quanto maggiore è l’inerzia del rotore e più alta è la
velocità di rotazione.
Occorre precisare che una direzione
fissa sulla Terra non è affatto fissa nello spazio, perché la Terra
ruota una volta sul proprio asse ogni 24 ore e compie una rivoluzione
completa attorno al sole ogni anno. Il sole stesso si muove nello
spazio portando con sé la Terra e gli altri pianeti. A causa di
questi movimenti, l’ espressione “direzione fissa nello spazio”
è quindi teorica. In ogni caso, da un punto di vista pratico è
possibile dire che una linea condotta dalla Terra a una stella
lontana (quella contenente l’asse di spin) è una direzione fissa
nello spazio. Se l’asse di rotazione di un giroscopio rotante è
puntato verso una stella lontana, rimarrà puntato verso la stella
mentre la Terra gira.
Ogni volta che si tenta di allontanare l’asse di spin dalla sua posizione iniziale, ad esempio applicando una forza F verticale (ved. disegno), a cui corrisponde un momento M, che darebbe luogo, se il rotore fosse fermo, ad una rotazione intorno ad un asse normale al piano di F (nell’esempio intorno all’asse YY), si sperimenta invece un secondo fenomeno detto precessione del giroscopio in cui l’asse di spin si sposta nel piano perpendicolare a quello contenente la forza perturbante. L’asse di spin cerca di raggiungere il vettore M (percorrendo l’angolo minore), ma quest’ultimo nel frattempo cambia direzione . Così l’asse di spin nell’inseguire il momento perurbante viene a descrive lentamente un cerchio come si può osservare chiaramente nel moto della trottola.
Foucault ebbe l’occasione di notare che il giroscopio con due gradi di libertà presentava proprietà applicabili in navigazione. Ad esempio notò che impedendo la rotazione intorno a Z, l’asse di spin, una volta disposto nel piano meridiano, si disponeva parallelo all’asse terrestre ndicando la latitudine del luogo.
Note sui vettori: Velocità angolare e momento di una forza sono grandezze fisiche vettoriali, cioè grandezze dotate sia di un valore sia di una direzione e verso, come le velocità, gli spostamenti, le forze. Per la velocità angolare e il momento di una forza, si assume per convenzione come positivo il senso di rotazione antiorario. In tal caso il vettore velocità angolare o il vettore momento sarà orientato perpendicolarmente al piano di giacitura della coppia di forze o dell’elemento rotante e il verso sarà diretto verso l’osservatore . Una semplice regola pratica che permette di stabilire direzione e verso di una velocità angolare o di un momento di forze è la regola della mano destra: se si dispongono le dita secondo il senso di rotazione della coppia o dell’elemento rotante, il pollice indica la direzione e il verso del momento o della velocità angolare.